publications

2022

2022

1. 

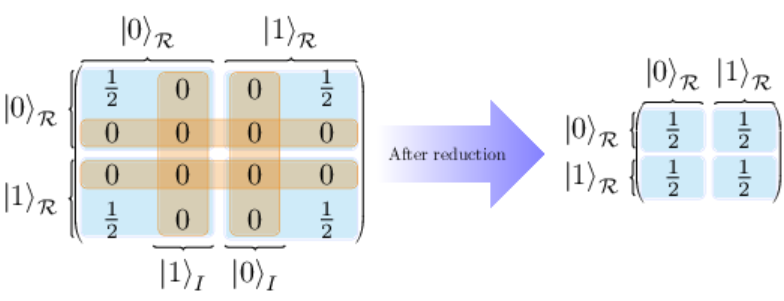   Entanglement Islands from Hilbert Space Reduction

   Debarshi Basu, Qiang Wen, and Shangjie Zhou

   Nov 2022

   Abs arXiv Bib

   In this paper we try to understand the Island formula from a purely quantum information perspective. We propose that the island phase is a property of the quantum state and the Hilbert space where the state is embedded in. More explicitly we show that, in a quantum system when the state of a subset is totally encoded in the state of another subset, the Hilbert space of the system will reduce, and the way we compute the reduced density matrix and related entropy quantities will also change essentially. Such reductions of the Hilbert space result in a new island formula in quantum systems, which we conjecture to be the same island formula in gravity recently proposed to rescue the unitarity in the process of black hole evaporation. In this context, we give a simple resolution to the Mathur/AMPS paradox. Furthermore, we propose a non-gravitational field theory configuration where entanglement islands emerge, give a description for the entanglement structure of the island phase and propose how to realize the island phase in the lab.

   @article{Basu:2022crn,
     author = {Basu, Debarshi and Wen, Qiang and Zhou, Shangjie},
     title = {{Entanglement Islands from Hilbert Space Reduction}},
     month = nov,
     year = {2022},
   }

2. 

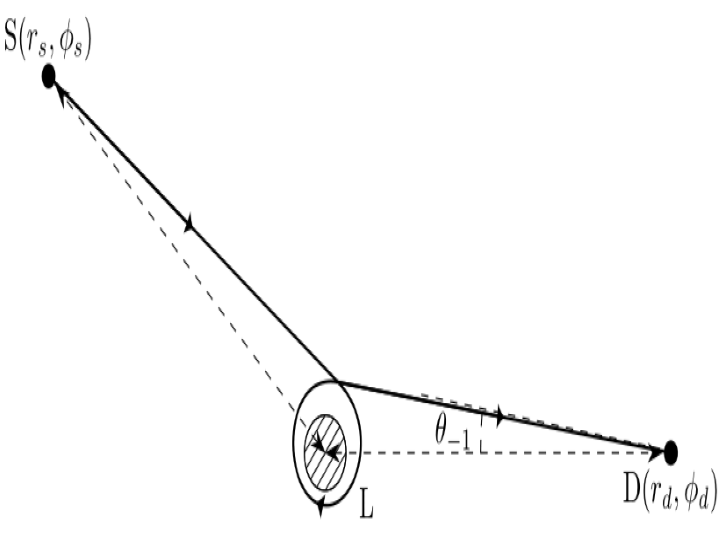   Effect of electric interaction on the deflection and gravitational lensing in the strong field limit

   Shangjie Zhou, Muchun Chen, and Junji Jia

   Eur. Phys. J. C, Mar 2022

   Abs DOI arXiv Bib

   The deflection angle ∆φof charged signals in general charged spacetime in the strong field limit is analyzed in this work using a perturbative method generalized from the neutral signal case. The solved ∆φnaturally contains the finite distance effect and takes a quasi-power series form with a logarithmic divergence at the leading order. The coefficients of the series contain both the gravitational and electric contributions. Using the Reissner-Nordström spacetime as an example, we found that an electric repulsion (or attraction) tends to decrease (or increase) the critical impact parameter b_c. If the repulsion is strong enough, then b_c can shrink to zero and the critical particle sphere r_0c will disappear. These results are applied to the gravitational lensing of charge signal, from which we solved the image positions, their magnifications and time delays. It is found that in general, the electric repulsion (or attraction) will decrease (or increase) the image apparent angles, the black hole shadow size as well as their magnifications but increase (or decrease) the time delay.

   @article{Zhou:2022dze,
     author = {Zhou, Shangjie and Chen, Muchun and Jia, Junji},
     title = {{Effect of electric interaction on the deflection and gravitational lensing in the strong field limit}},
     month = mar,
     year = {2022},
     journal = {Eur. Phys. J. C},
     volume = {83},
     number = {9},
     pages = {883},
     doi = {10.1140/epjc/s10052-023-12047-z}
   }